This page discusses (at some length!) how the concept of "optimum phasing" works out for overhead lines where the conductor bundles (or phases) are arranged in a triangle rather than a straight line. See our main page on phasing including details of the UK policy to adopt optimum phasing.
 This is prompted by the introduction by National Grid of the T-pylon, an example of exactly this triangular arrangement, but the principles hold true for any other triangular arrangement.
This is prompted by the introduction by National Grid of the T-pylon, an example of exactly this triangular arrangement, but the principles hold true for any other triangular arrangement.
Phasing for linear arrays
First, a recap on how optimum phasing works for traditional lattice pylons, where the phases for each circuit are roughly in a straight line, or a "linear array".
"Untransposed" phasing has the same order of the three phases on the two sides of the pylon (the two circuits), and the magnetic fields are in the same direction and reinforce each other:
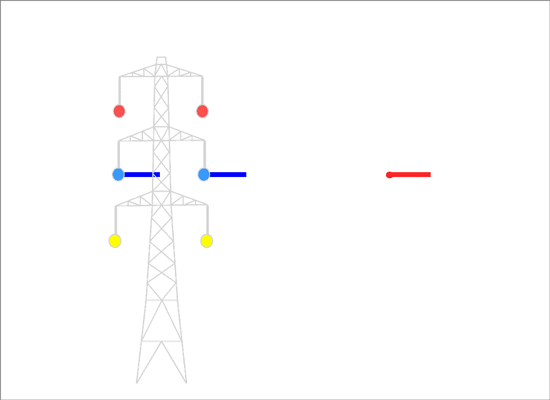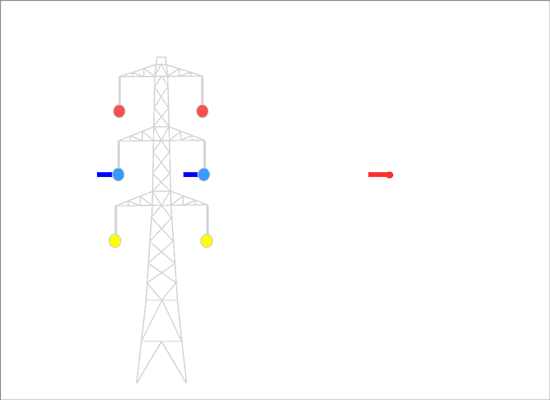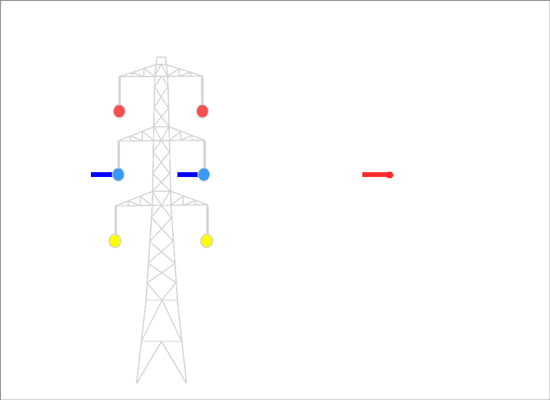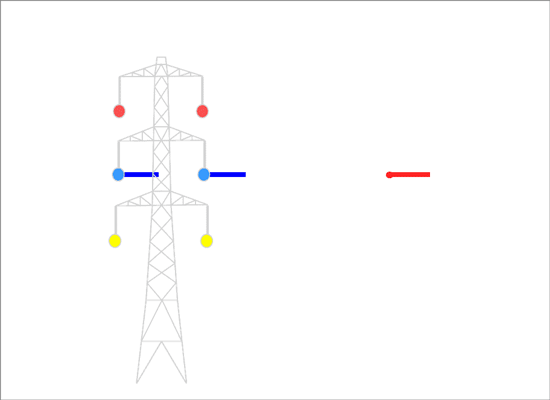
Note: to illustrate the principles as clearly as possible, we've simplified a bit - we've considered circuits that are exactly vertical rather than sloping slightly because of the taper of the pylon, and we're considering the field level with centre of the conductors rather than at ground level. Both of those factors introduce some elliptical polarisation rather than the linear polarisation we show here. You can see this in more detail on a separate page.
"Transposed" phasing has the order of the phases in the opposite direction on the two sides. The fields are in opposite directions (exactly so in this simplified diagram, very nearly so for real-life pylons which tend to have a slight taper) and there is partial cancellation:
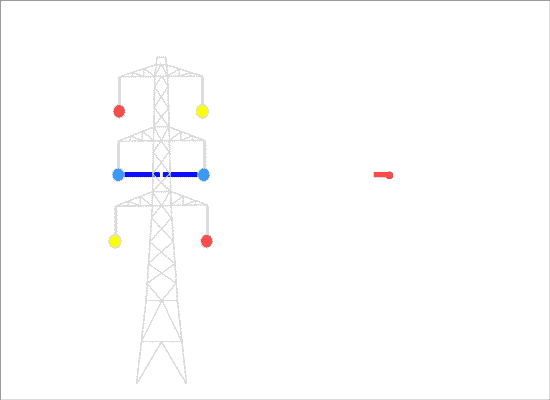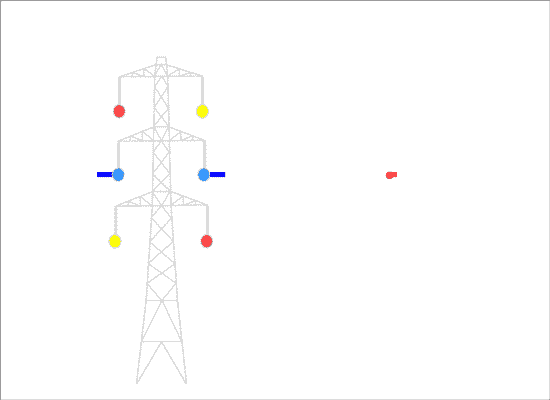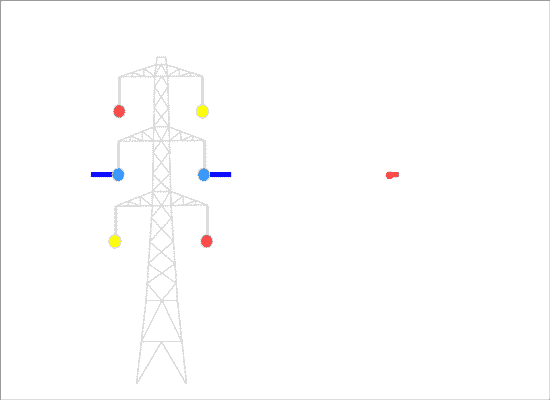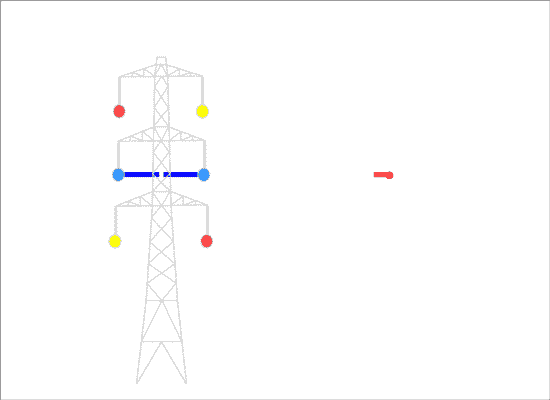
This produces a lower overall field to the sides of the line, so we call it "optimum" phasing.
Phasing for triangular arrays
Linear arrays (as above) produce linear fields. The key difference is that triangular arrays produce fields that rotate instead of just oscillating backwards and forwards in a straight line - "elliptical polarisation". For any triangle, the field goes round an ellipse. For the phases in an equilateral triangle, which is what we will consider here for simplicity, the field goes round an exact circle.
With two triangular arrays, suppose we fix the order of the phases on one side (the left side for convenience). There are then, mathematically, six different possible orders of the phasing on the other side. They each produce a different field as shown here:
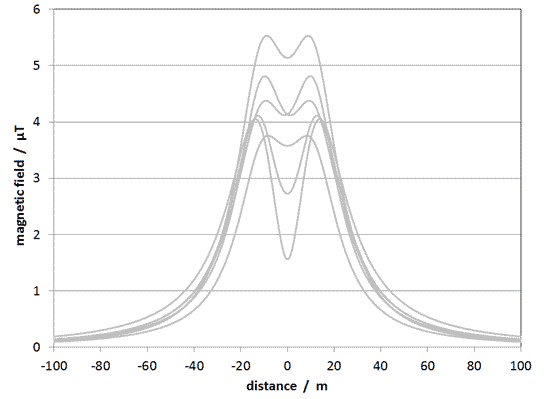
Note: the purpose of this graph is to show how changing the phasing changes the field. So the absolute values of field aren't so important. But in fact, this graph is calculated for the same conditions we use to illustrate all the other factors affecting the field from power lines - 12 m ground clearance and 500 A per circuit, fairly typical of normal conditions for UK power lines.
We will return to this graph later and make sense of all the various different curves.
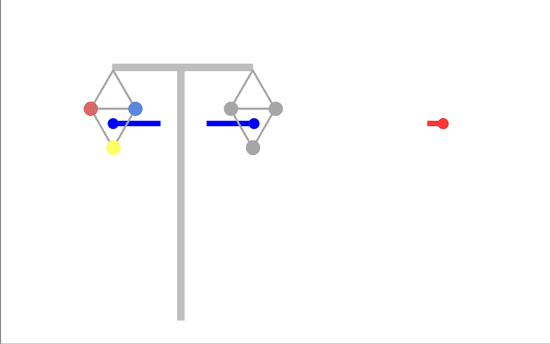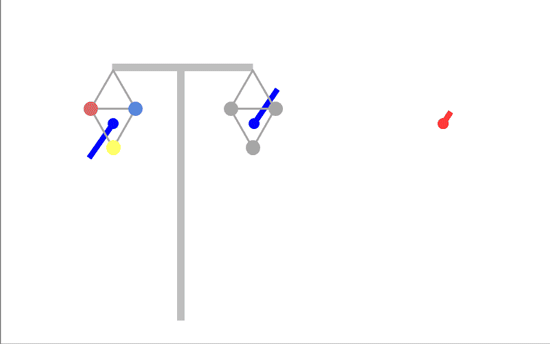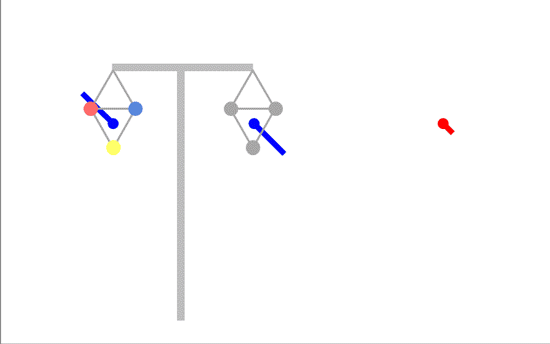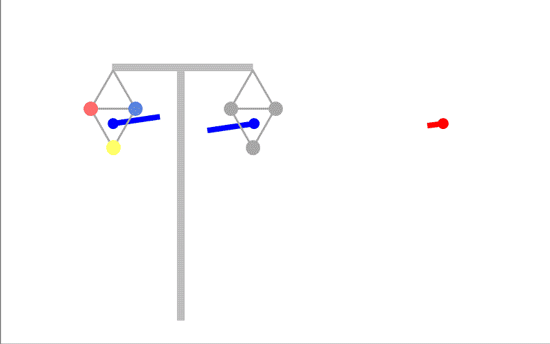
The magnetic field from each circuit rotates in a circle, but just as for the linear arrays, the worst case is untransposed phasing, with the same order of phases on the two sides. Then the two fields rotate in the same way, reinforcing each other:
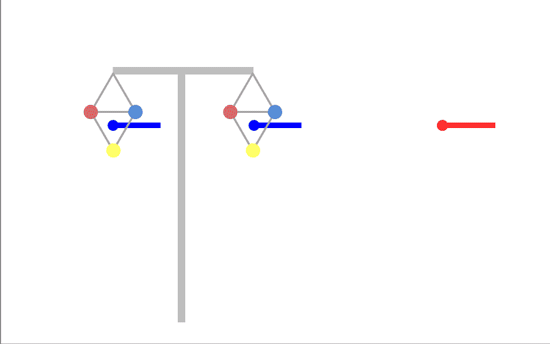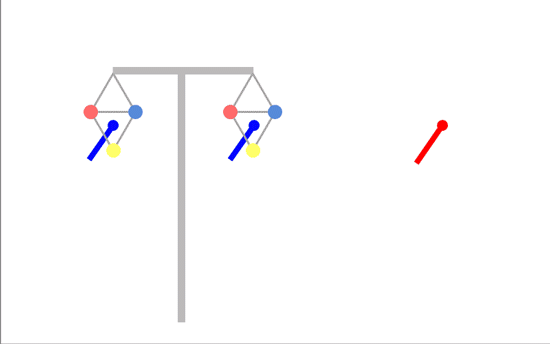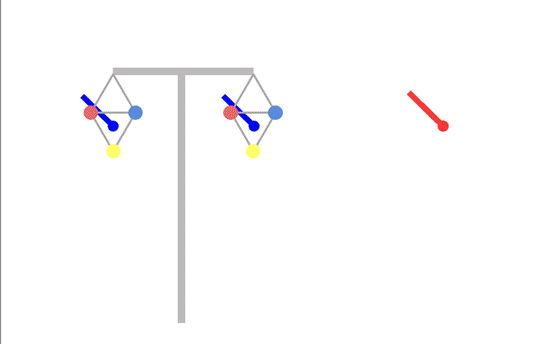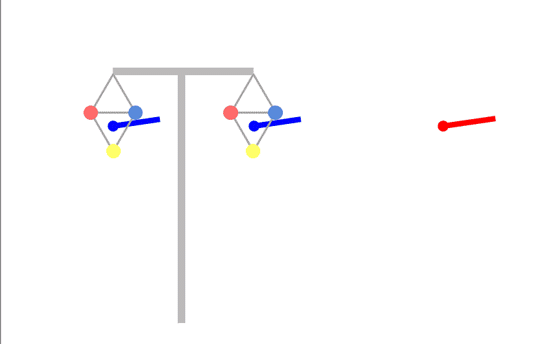
(please note that these diagrams are designed to show the principles at work and are not to scale - the resultant field to the sides is actually a lot smaller because of the way fields fall with distance, so we've amplified it so you can see what is happening more clearly.)
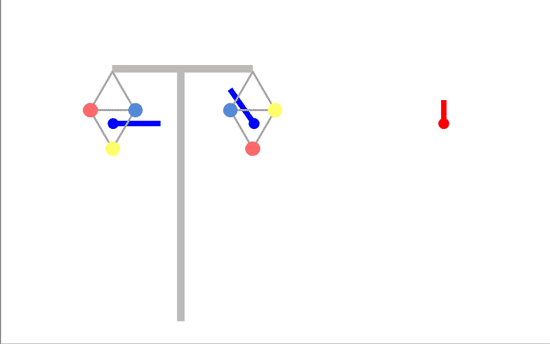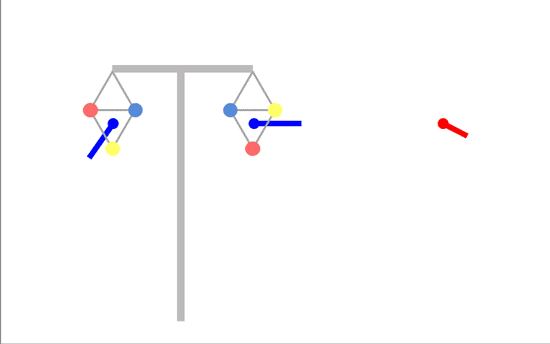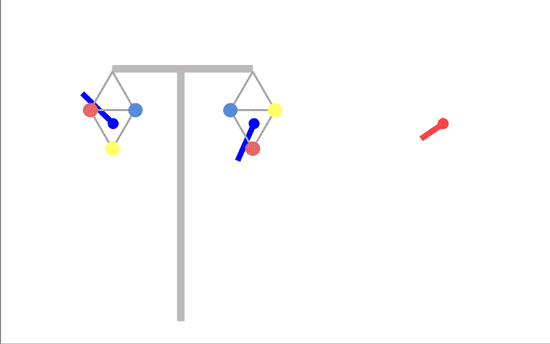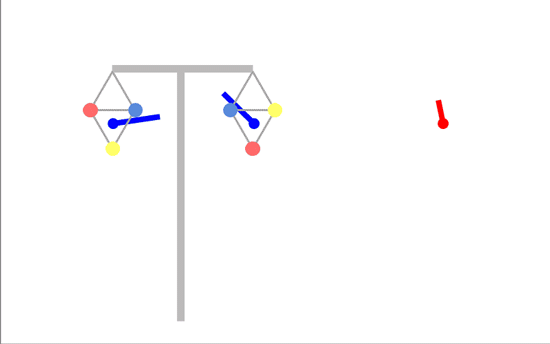
But now consider transposed phasing (which was the best option for linear arrays):
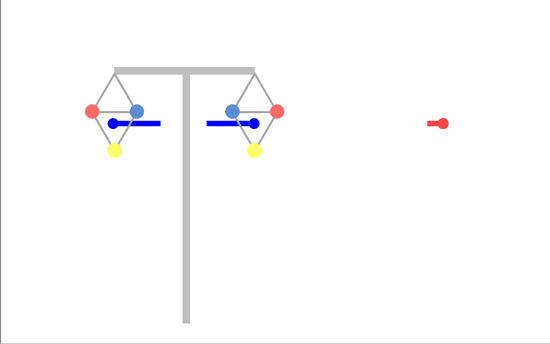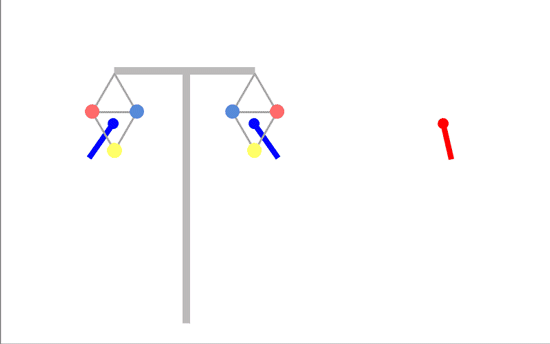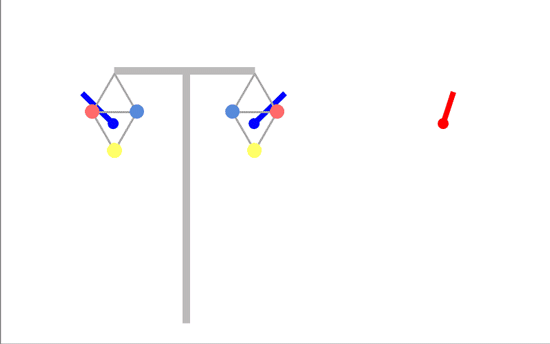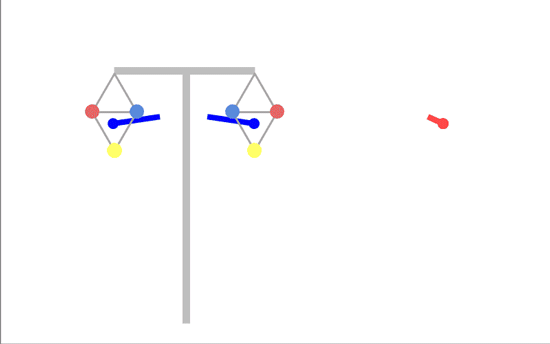
The horizontal components of the field are behaving exactly as they did for the linear array - they are opposing each other and partly cancel each other (you are closer to one circuit than the other, so the field from that circuit is stronger, so the cancellation isn't perfect). But the vertical components are reinforcing each other. This means transposed phasing is not actually the optimum phasing for triangular arrays.
The best phasing would be if we could have the two fields exactly opposite each other (180 degrees apart) and rotating the same way:
Unfortunately, you can't achieve this with a T-pylon or similar - you'd need conductors on one circuit positioned half way between where they actually are - the triangle pointing up instead of down.
The best we can do is to have the two fields 120 degrees apart instead of the ideal 180 degrees (in this diagram, the field from the right-hand circuit is following the field from the left-hand circuit round but 120 degrees behind it):
To show the effect of these options, this graph shows the same six possibilities as before, but highlighting these three in particular:
- untransposed, clearly the worst to the sides;
- transposed, better but not the best;
- and the optimum.
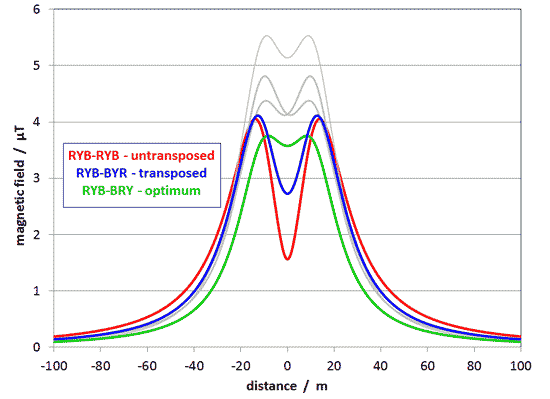
Note that we are concerned with reducing the field to the sides of the line, where people are most likely to live or to spend time. Close to the line, and in particular between the two circuits, the relative merits can actually reverse - this often happens with phasing and we explain why on a separate page.
Summary so far
- The optimum phasing for T-pylons isn't transposed phasing, it's another arrangement with the fields 120 degrees apart
- In any event, optimum phasing can never work as well for T-pylons as for traditional lattice towers
The next two drop-down boxes now go on to explain what happens to the phasing when you need to transition between different types of pylon.
Simultaneous phasing of lattice pylons and T-pylons
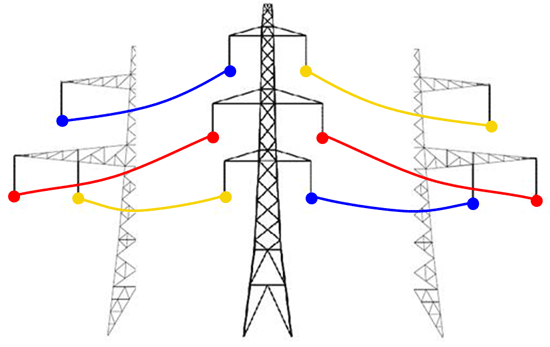
In some of the situations where the T-pylon is being proposed, the entire route is proposed as T-pylons. But in some situations, there is a transition from traditional lattice pylons to T-pylons part way along the route. You can only transition the phases from one to the other in one specific order, because of the need to preserve the clearances between the phases as they cross from one geometry to the other: top phase on the lattice has to go to inside top of the T-pylon and so on. This is shown in this diagram:
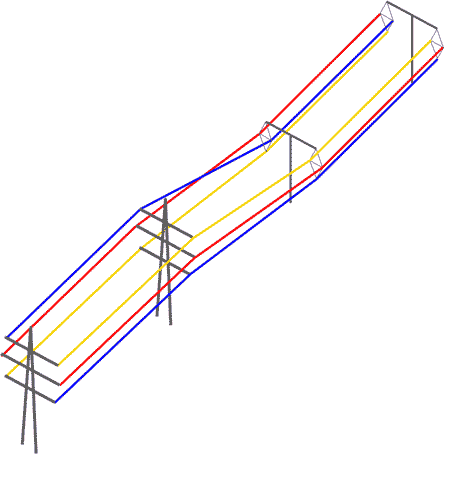
Or, if it's easier to see the details, this end-on diagram:
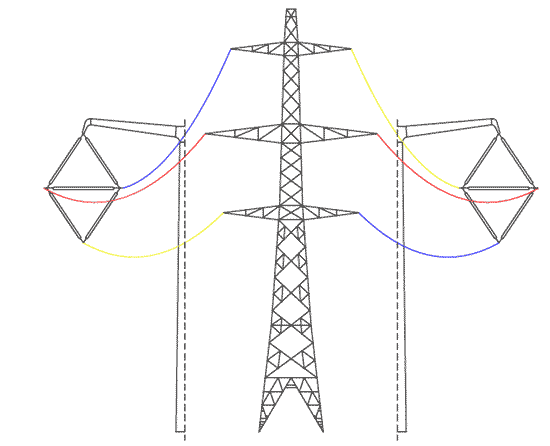
Unfortunately, this means that you cannot have optimum phasing for the lattice and the T-pylon simultaneously - you have to prioritise one or the other.
Which should you prioritise? There are two reasons to prioritise the phasing of the lattice pylons. The first is that they produce a higher field to start with. This graph compares the fields of the two designs with untransposed phasing, that is, the "raw" field they each produce before any reduction by phasing:
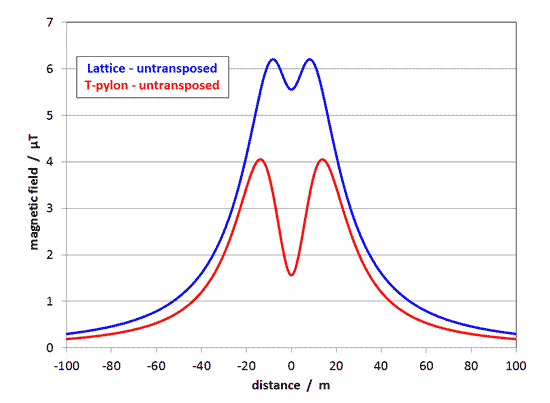
The second reason is that, as explained higher up this page, phasing is more effective for the lattice pylon than for the T-pylon. Whatever phasing you chose for the T-pylon, it wouldn't produce as big a reduction to the sides of the line as transposed phasing does for the lattice pylon.
So the correct thing to do to get the best overall optimisation is usually to optimise the lattice section and let the phasing of the T-pylon be dictated by that. (There might be exceptions if the lattice section was very short and the T-pylon section very long.)
If we do that, what phasing do we end up with for the T-pylon? You can see this from the diagrams of the transition above. If the lattice is transposed phasing with BRY-YRB (top to bottom), the T-pylon will be RYB-YBR (left to right). The field from this phasing is shown on this graph in comparison to the optimum phasing for the T-pylon alone:
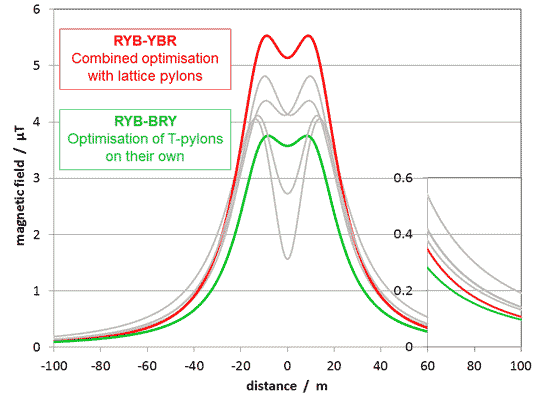
Between the circuits, the situation is different, as we've said before. But to the sides of the lines, which is where we're mainly concerned with, the phasing we end up with is actually not too bad. It's the second lowest of the six options, and the further out you go, the closer it gets to the ultimate optimum.
More detail on how these two phasings compare
We said that the best phasing for the T-pylon is where the magnetic fields from the two circuits follow each other round 120 degrees apart:

There are two different ways of achieving this. As you rotate clockwise round the triangle of the three phases, the order has to be R-B-Y. But you can do this in two different ways:
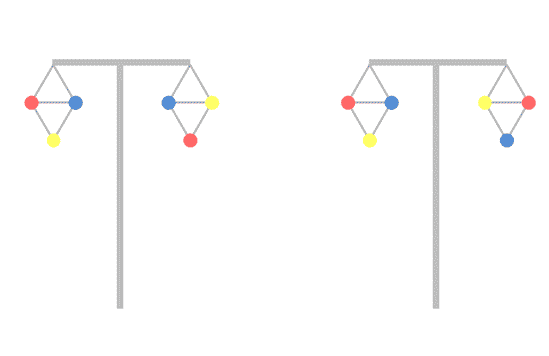
The one on the left is the one that is the optimum for the T-pylon on its own. But the one on the right just so happens to be the phasing you get when you optimise the lattice pylons.
To complete this story and explain why these two aren't exactly the same, we now need to unpick the assumptions we've been making just a little bit more. All this modelling of fields as rotating in circles is true when you are quite a bit further away from the conductors than the distance between them, so that you can treat the array of three phases as a single source and not have to worry about the contribution of the individual phases. Obviously, the further away you get, the more true this becomes. This is why the field for the combined optimum phasing converges on the field for the T-pylon-alone optimum phasing, and if we extended the calculation to even larger distances, they would become exactly the same, because they are both producing fields that are 120 degrees apart. And this means that the "rotating vectors" diagram - which shows what happens at large distances - is actually the same for these two options. But when you are closer to the line itself, you cannot just rely on the circular-rotation approximation, you have to start taking account of the individual phases. And, as can be seen from the diagram above, the relationship of the individual phases looks quite different when you're close to them. That is why the T-pylon-alone optimum phasing produces lower fields than the combined optimisation. But the combined optimisation is still better than any of the other options.
Summary
To sum up this whole story:
- The optimum phasing for T-pylons isn't transposed phasing, it's another arrangement with the fields 120 degrees apart
- In any event, optimum phasing can never work as well for T-pylons as for traditional lattice towers
- When you have a line that is part lattice pylons and part T-pylons, the best thing to do is to optimise the phasing of the lattice section, and let that determine the phasing of the T-pylon section
- When you do that, it turns out that the resulting phasing for the T-pylon is in fact almost as good as the true optimum
- And, underlying all this, the T-pylon produces a lower field to start with. All fields from all power lines comply with the relevant exposure limits in the UK.
Simultaneous phasing of lattice pylons and low-height pylons
 The discussion above was about what happens to the phasing when you transition from the traditional lattice pylon, with vertical circuits, to the T-pylon, with triangular arrays. But there's another design of pylon with triangular arrays - the low-height pylon.
The discussion above was about what happens to the phasing when you transition from the traditional lattice pylon, with vertical circuits, to the T-pylon, with triangular arrays. But there's another design of pylon with triangular arrays - the low-height pylon.
The same thing happens as with the T-pylon: if we start with the traditional lattice having transposed phasing, we end up with the low-height lattice having the magnetic fields following each round 120 degrees apart, which we said was the best that could be achieved with triangular arrays:

There's one more sublety. There are two different ways of having the magnetic fields 120 degrees apart. They both deliver the same benefit of reduced fields at large distances, but they differ at closer distances. For the T-pylon, the one we end up with when we start with a transposed lattice was the less good one at closer distances - overall, the second best out of the six phasing options rather than the best. But for the transition to the low-height pylon, the option we end up with turns out to be the best.
In other words, when transitioning from a traditional lattice to a low-height lattice pylon, both can have optimum phasing.
Unlike the T-pylon, which hasn't been built and connected to another pylon yet, low-height pylons do exist. Here is how the transition looks in reality, first from side-on:

Then standing at the traditional lattice and looking along the transition span to the low-height lattice:

Other aspects of phasing
- Our main page on phasing, including the UK policy on phasing
- What happens between the circuits and why the optimum phasing can produce bigger fields there
- The extent of phasing in the UK
Elliptical polarisation
This page explains how linear arrays of conductors produce mainly linearly polarised fields and triangular arrays produce mainly elliptically polarised fields. But even linear arrays on traditional pylons end up producing fields that are to some extent elliptically polarised.
The field values
This page is mainly about how the phasing changes the field. See more on the actual field values from traditional 400 kV lattice pylons and from alternatives including the T-pylon.
Try it for yourself
You can use our online calculator to experiment with varying the phasing of both T-pylons and traditional lattice pylons and see what effect it has on the magnetic field.