What happens when you have two magnetic (or two electric) fields from different sources and you need to add them together to work out what the total is?
With many other things - chemicals, or ionising radiation, for example - the answer is easy. The sum of a and b is a+b.
This is not true for magnetic fields because magnetic fields are vectors - they have direction as well as size. The sum of a and b is only a+b if the two vectors are exactly in line. Usually they are not in line and the resultant is less than a+b.
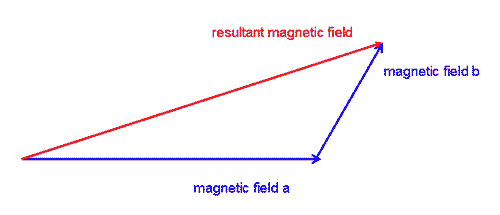
In fact, the field b can vary in orientation over all the possible directions relative to the field a. So the resultant can actually lie anywhere on a sphere, radius b, centred on the end of a.
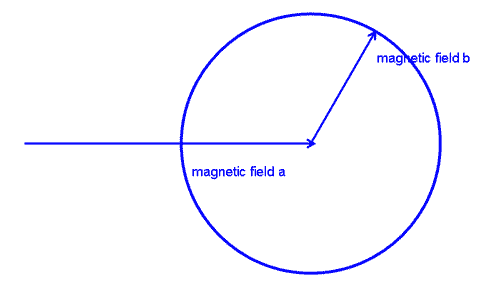
Usually, if the two fields come from different sources, the orientation is random and will vary over time. So, over the course of time, the resultant does actually vary over the whole surface of the sphere. Intuitively, it makes sense that the average direction and hence the average value of the resultant is when the two vectors are at right angles.
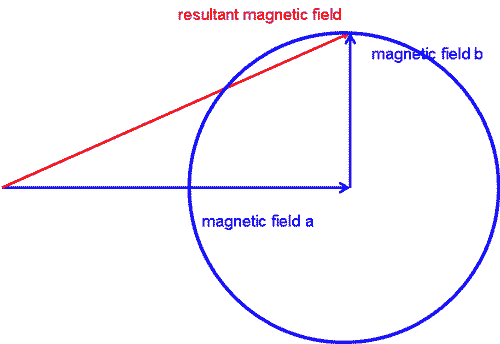
When the two fields are right angles the resultant has a magnitude (a2+b2)1/2. A rigorous derivation shows that when two fields have random orientation, the root-mean-square of the resultant is indeed given by this formula, but the mean of the resultant is slightly less. You can download a copy of this derivation here: additionofmagneticfields.
What does this mean in practice?
If you have two magnetic fields a and b with random orientation (or, which comes to the same thing, random phases), the average magnitude is given by (a2+b2)1/2. This means that one field has to be only slightly larger than the other to dominate the result. For example, if field b is half the size of field a, it makes only a 10% difference to the total. Therefore, in practice, if we want to know what the field is at a given place, we need usually assess the field from the biggest single source only, and don't have to bother with all the smaller contributions.
People often use this result when talking about EMFs without being explicit. For instance, if we are talking about a power line, we will often calculate the field from the power line and ignore other sources. That is indeed a valid thing to do, but only because of this result about adding vectors.